
地球は丸いことは公然の事実ですが、2020年においても宇宙の形について結論は出ておらず、いまだ大きなテーマとなっています。宇宙の形は具体的にどのようなものとして考えられているのかを「三角形の角度」という観点から、数学および科学専門のジャーナリストであるエリカ・クラライヒ氏が解説しています。
What Is the Geometry of the Universe? | Quanta Magazine
https://www.quantamagazine.org/what-is-the-geometry-of-the-universe-20200316/
◆「宇宙は平ら」だとする説
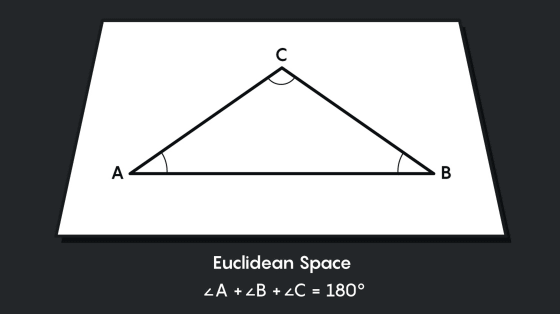
宇宙の形についての仮説の1つに、「宇宙はユークリッド幾何学の空間にあり平らである」という説があります。ユークリッド幾何学においては、直線はどこまでも伸び、平面どこまでも平らで、平行線は交わることなく平行であることが想定されます。この空間内では三角形はまっすぐな線で描かれるため、角度の和は180度になります。
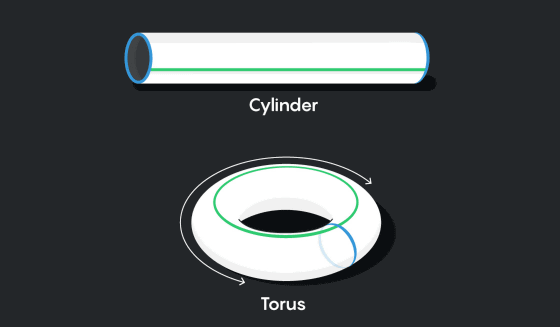
平らな宇宙を視覚化するのは難しく、3次元ではなく2次元空間から捉えることで分かりやすくなります。まず、長方形状の平面をイメージし、次に、その上端と下端をくっつけて円柱にします。

次に、円柱の両端をくっつけてドーナツ形のトーラスを作成します。
そして、トーラスの内側に、ループして開始位置に戻る3種類の線をイメージします。1つは長方形の長辺に対して平行な線、1つは長方形の短辺に対して平行な線、もう1つは長方形の対角線を結ぶ直線です。
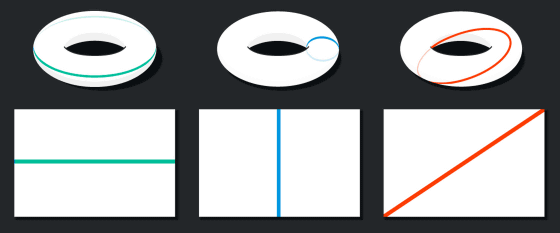
3種類の線は、トーラス上ではカーブしているように見えますが、平面で考えるとまっすぐな線になります。トーラス内で光もまたまっすぐな線に沿って進むため、トーラスの内側に立っている人間が光の進む方向をまっすぐ見ると、自分の姿を背面から見ることができるとのこと。
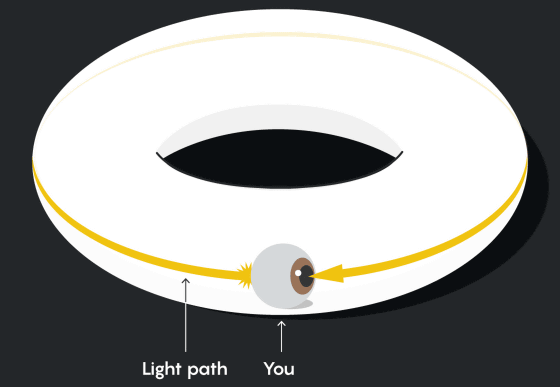
つまり、トーラス内部では、自分の姿を背面から見ることができる、さまざまな方向の光のループがあることになります。
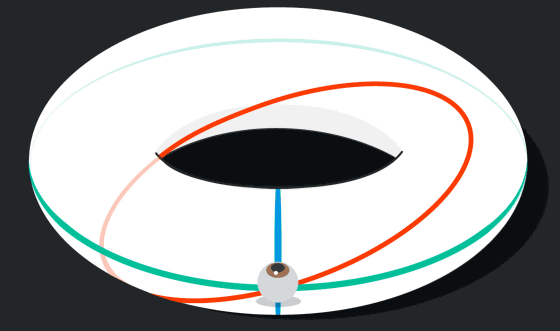
トーラス内の状況を平面に戻してみると、例えば自分の前から後ろに向かって進む光は、後ろに達したら再び前に戻ってくるというループを繰り返します。
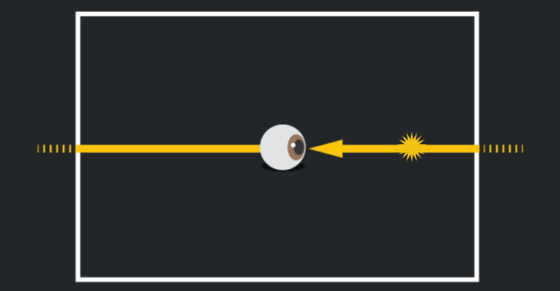
平面を1つの部屋に例えると、前から後ろに向かって進む光のループによって、自分の前後に部屋と自分の像が作り出されたような状態になります。前から後ろだけでなく、自分から自分に戻るさまざまな方向の光のループによって、無数の部屋と自分の像を見ることができます。
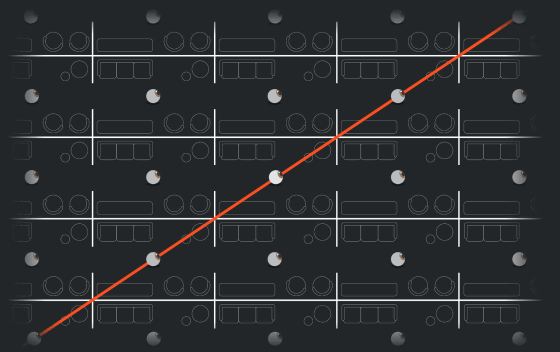
厳密には、宇宙は平面ではなく、直方体のボックスが連続して続くトーラスであると考えられています。この空間を視覚化することはできませんが、その中にいる生物についてイメージすることはできます。
1つの平面を部屋に例えたとき、平面のトーラスにいた人間が同一の長方形の部屋が無限に続く中に住んでいたように、3次元トーラス内の人間は同一の長方体が無限に続く部屋の中に住んでおり、あらゆる方向に自分自身のコピーが無限に見えているということになります。

このため、人間の目から見ると、宇宙は同じものが無限に連なっているように見えるのはずなのですが、実際の宇宙に目を向けると、自分自身のコピーを無限に見ることはできません。なぜなら、宇宙は広大で、同じ光が人間に届くまでには途方もなく長い時間を要するためです。
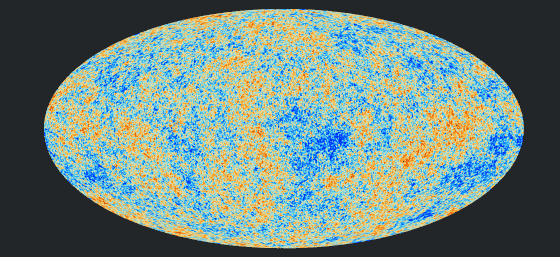
そのため、「宇宙が平らであること」を証明するために、天文学者は宇宙で自分自身のコピーが見られる光を探すのではなく、宇宙で見ることができる最も遠くにあるもの、つまりビッグバン直後に残った宇宙マイクロ波背景放射(CMB)の連続を探しています。
つまり、温度分布のイメージマップにおいて、異常に温度が高い赤色のエリア(ホットスポット)と異常に温度が低い青色エリア(コールドスポット)が同じパターンになるCMBを探索することを意味しています。同じパターンのCMBが、異なる2つの方向で発見されたとき、宇宙が平らであることが示唆されます。
◆「宇宙は球状」だとする説
宇宙で三角形を測定することは、天文学者が「宇宙が曲がっているかどうか」をテストする重要な方法の1つです。宇宙の形が球状、つまり、地球と同じような球状であると考えた場合、平らな宇宙とは異なり、測定によって検出された宇宙の地点から三角形の角を合計することで、宇宙の形を証明することができます。球面幾何学では直線は大円を描き、三角形は膨らんだような形になり、3つの角を合計すると180度以上になります。
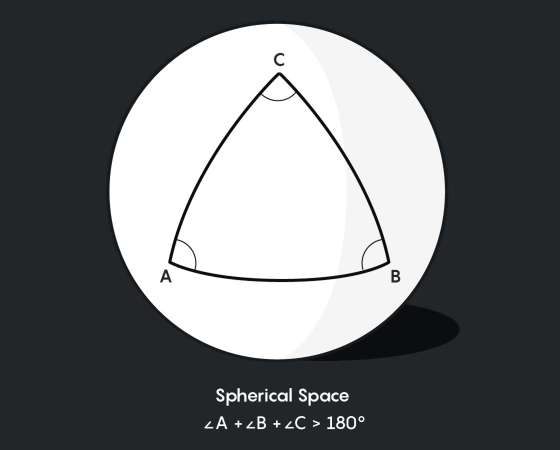
球面幾何学では直線は大円であることから、CMB中にあるホットスポットまたはコールドスポットをつなぐ大円を直線として大円を計測します。その大円から、地球の位置を基準にして三角形を測定し、三角形の辺の長さと角度から、三角形の角の和が180度以上であるかどうかを計算します。
2018年の研究では、人工衛星プランクから得られたデータの一部から「宇宙は球状である」と主張されましたが、他の研究者たちは「統計上の誤差である」と反論しています。
◆「宇宙は双曲平面」だとする説
以下の図は、ポワンカレの円板と呼ばれる双曲平面の図です。宇宙はポワンカレの円板のように広がっているという説があります。

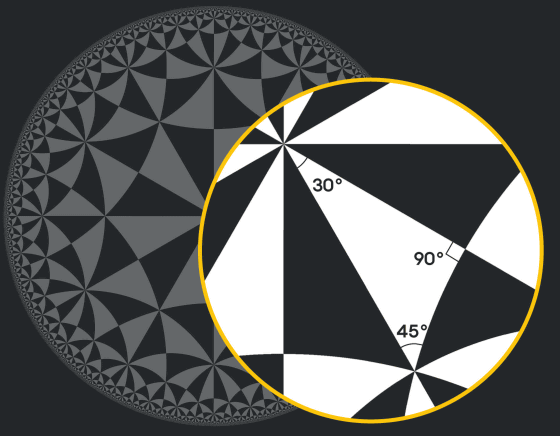
平面の図で見ると、外側にある三角形ほど小さく見えますが、双曲幾何学の視点からは、すべての三角形が同じサイズであると捉えます。円の境界はあらゆる方向に無限に広がっており、境界近くの三角形の数は指数関数的に増加します。

また、双曲幾何学においては、三角形の角度の合計は180度未満です。たとえば、以下のポワンカレの円板上の三角形の角度の合計は30度+90度+45度=165度になります。
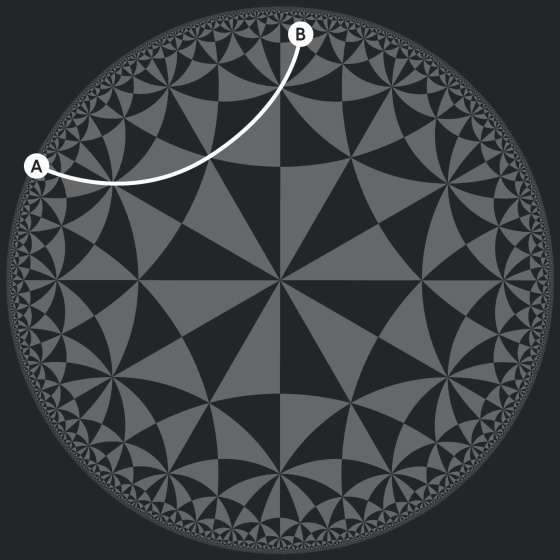
これらの三角形の辺はまっすぐに見えませんが、これは双曲幾何学を無理やり平面上に表していることから、歪んだレンズを通したようになっているため、ポワンカレの円板上で生きている生物にとっては、この曲線は直線に見えており、AからBの最短ルートは以下のようになります。
記事作成時点では、宇宙は平らであるという説が支持されています。しかし、クラライヒ氏は「球面や双曲幾何学のどちらかである可能性を否定することはできません」と語ります。なぜなら宇宙は広大で、球面幾何学あるいは双曲幾何学上の三角形の合計角度は、平面の宇宙における三角形の合計角度との差が非常に小さいとされているためです。
クラライヒ氏は、「もし宇宙が非常に大きな球形や双曲形であるとすれば、現代の技術で観察できる部分は限りなく平坦に近く、その曲率は人類がまだ発明していないような超精密な装置でしか検出できないでしょう」と述べ、宇宙の形を解き明かすにはまだまだ時間がかかると主張しています。
この記事のタイトルとURLをコピーする
"形" - Google ニュース
March 22, 2020 at 02:00PM
https://ift.tt/2wsl2BG
三角形の角度から分かる「宇宙の形」とは? - GIGAZINE
"形" - Google ニュース
https://ift.tt/2NVTTwG
Shoes Man Tutorial
Pos News Update
Meme Update
Korean Entertainment News
Japan News Update
No comments:
Post a Comment